next up previous contents
Next: Mass Matrix Up: Two Dimensional Element Mechanics Previous: Kinematic Description

Strain-Displacement Matrix

As mentioned in the previous section, the following definition of the strain vector is required to support the selective reduced integration

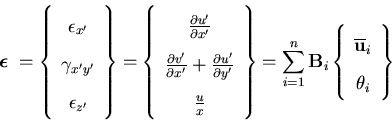\begin{displaymath}{\mbox{\boldmath$\epsilon$ }}= \left\{\begin{array}{c} \e... ...} \overline{{\bf u }}_i \\ \theta_i \end{array} \right\} \end{displaymath}(60)

in which 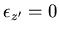$\epsilon_{z'}=0$ in case of plane shell. This definition yields the following strain-displacement matrix

\begin{displaymath}{\bf B}_i = \left[ \begin{array}{cc} {\bf B}^u_{MN} & B^\th... ...ta_{TS} \\ {\bf B}^u_H & B^\theta_H \end{array} \right] \\ \end{displaymath}(61)

where the subscript H denotes the hoop strain components which are non-zero only in case of axisymmetric shell. In order to find the strain displacement matrix, the displacement vector given by Equation (2.58) is transformed to the lamina coordinate system. Thus,

\begin{displaymath}{\bf u'}=\sum_{i=1}^{n} N_i (\xi) \left[ {\bf q} \overline{{\bf u}}_i + \frac{t_i \eta }{2} {\bf q R_i} \theta_i \right] \end{displaymath}(62)

Taking the derivative of 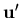${\bf u'}$ with respect to x' and y' gives
$\displaystyle \frac{\partial {\bf u'}}{\partial x'}$=$\displaystyle \sum_{i=1}^{n} \left[ \frac{\partial N_i }{\partial x'} {\bf q} \... ...rac{\partial\left( \eta N_i \right) }{\partial x'} {\bf q R_i} \theta_i \right]$(63)
$\displaystyle \frac{\partial {\bf u'}}{\partial y'}$=$\displaystyle \sum_{i=1}^{n}\left[ \frac{\partial N_i }{\partial y'} {\bf q} \o... ...rac{\partial\left( \eta N_i \right) }{\partial y'} {\bf q R_i} \theta_i \right]$(64)

Thus, the components of the strain-displacement matrix are given as
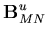$\displaystyle {\bf B}^u_{MN}$=$\displaystyle \left[ \begin{array}{cc} \frac{\partial N_i}{\partial x'} & 0 \end{array}\right] {\bf q}$(65)
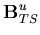$\displaystyle {\bf B}^u_{TS}$=$\displaystyle \left[ \begin{array}{cc} \frac{\partial N_i}{\partial y'} & \frac{\partial N_i}{\partial x'} \end{array}\right] {\bf q}$(66)
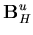$\displaystyle {\bf B}^u_H$=$\displaystyle \left[ \begin{array}{cc} \frac{N_i}{x} & 0 \end{array}\right]$(67)
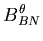$\displaystyle B^\theta_{BN}$=$\displaystyle \frac{t_i }{2} \left[ \begin{array}{cc} \frac{ \partial \left(\eta N_i \right) }{\partial x'} & 0 \end{array}\right] {\bf q}{\bf R}_i$(68)
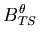$\displaystyle B^\theta_{TS}$=$\displaystyle \frac{t_i }{2} \left[ \begin{array}{cc} \frac{\partial \left(\eta... ...rtial \left(\eta N_i \right) }{\partial x'} \end{array}\right] {\bf q}{\bf R}_i$(69)
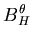$\displaystyle B^\theta_H$=$\displaystyle \left[ \begin{array}{cc} \frac{\eta t_i N_i }{2x } & 0 \end{array}\right] \left\{ R_i\right\}$(70)

next up previous contents
Next: Mass Matrix Up: Two Dimensional Element Mechanics Previous: Kinematic Description
A. Zeiny
2000-09-06