Kinematic Description

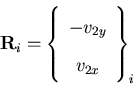
Next: Strain-Displacement Matrix Up: Two Dimensional Element Mechanics Previous: Geometric Description

Kinematic Description

The kinematics of the plane shell element are defined also by invoking the isoparametric hypothesis which leads to

$\begin{displaymath}\left\{\begin{array}{c} u\\ v \end{array} \right\} = \su... ...ay} \right\} + \frac{t_i \eta}{2} {\bf R}_i \theta_i \right] \end{displaymath}$

(57)

or concisely

$\begin{displaymath}{\bf u}=\sum_{i=1}^{n} N_i (\xi) \left[ \overline{{\bf u}}_i + \frac{t_i \eta}{2} {\bf R}_i \theta_i \right] \end{displaymath}$

(58)

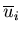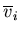where $\overline{u}_{i}$ and $\overline{v}_{i}$ are the middle surface displacements in the X and Y directions at node i, respectively, and 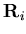${\bf R}_i$ is the rotation arm vector at node i given by

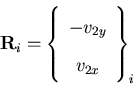$\begin{displaymath}{\bf R}_i = \left\{\begin{array}{c} -v_{2y}\\ v_{2x} \end{array} \right\}_i \end{displaymath}$

(59)

A. Zeiny
2000-09-06