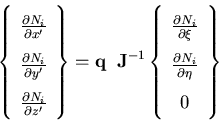
Next: Mass Matrix Up: Three Dimensional Element Mechanics Previous: Kinematic Description
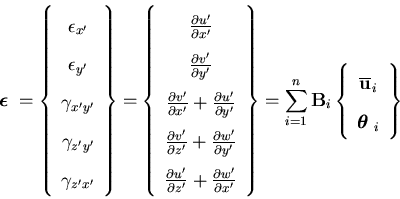
In application to shells, special attention needs to be given to transverse shear and membrane components to prevent the mesh locking phenomena. A particularly effective treatment may be performed by employing the reduced selective integration concept. In the present formulation, the strain-displacement matrix is formulated such that each component is separated from the others. This is achieved through the following definition of 
![\begin{displaymath}{\bf B} = [{\bf B}_1\; {\bf B}_2\; \cdots\;{\bf B}_n ]\\
\end{displaymath}](img120.gif) | (23) |
where n is the number of nodes per element. The strain-displacement transformation may be written as
 | (24) |
where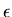 
is the strain vector with its components in the lamina coordinate system. The main reason behind this choice for the strain vector components is to facilitate the separation between various strain components. Therefore, the 
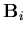matrix is written in the form
![\begin{displaymath}B_i = \left[ \begin{array}{cc}
B^u_{MN} & B^\theta_{MB} \\ ...
...a_{BS} \\
B^u_{TS} & B^\theta_{TS}
\end{array} \right] \\
\end{displaymath}](img123.gif) | (25) |
in which the subscripts MN, MB, MS, BS and TS denote membrane normal, membrane bending, membrane shear, bending shear and transverse shear components, respectively. In order to find these components the displacement vector given by Equation (2.19) is transformed to the lamina coordinate system. Thus,
![\begin{displaymath}{\bf u'}=\sum_{i=1}^{n} N_i (\xi,\eta) \left[ {\bf q} \overli...
... t_i}{2} {\bf q R_i} \mbox{\boldmath$\theta_i$\space } \right]
\end{displaymath}](img124.gif) | (26) |
taking the derivative of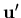 
with respect to x', y' and z' gives
Thus, the components of the strain-displacement matrix are given as
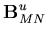 | = | ![$\displaystyle \left[ \begin{array}{ccc}
\frac{\partial N_i}{\partial x'} & 0 & 0 \\
0 & \frac{\partial N_i}{\partial y'} & 0
\end{array}\right]
{\bf q }$](img132.gif) | (30) |
 | = | ![$\displaystyle \left[ \begin{array}{ccc}
\frac{\partial N_i}{\partial y'} & \frac{\partial N_i}{\partial x'} & 0
\end{array}\right]
{\bf q }$](img134.gif) | (31) |
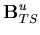 | = | ![$\displaystyle \left[ \begin{array}{ccc}
0& \frac{\partial N_i}{\partial z'} & \...
...{\partial z'} & 0 &\frac{\partial N_i}{\partial x'}
\end{array}\right]
{\bf q }$](img136.gif) | (32) |
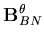 | = | ![$\displaystyle \frac{t_i}{2}
\left[ \begin{array}{ccc}
\frac{ \partial \left( \z...
...left( \zeta N_i \right) }{\partial y'} & 0
\end{array}\right]
{\bf q }{\bf R}_i$](img138.gif) | (33) |
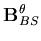 | = | ![$\displaystyle \frac{t_i}{2}
\left[ \begin{array}{ccc}
\frac{ \partial \left(\ze...
...\left(\zeta N_i \right) }{\partial x'} & 0
\end{array}\right]
{\bf q }{\bf R}_i$](img140.gif) | (34) |
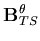 | = | ![$\displaystyle \frac{t_i}{2}
\left[ \begin{array}{ccc}
0& \frac{ \partial \left(...
...ial \left(\zeta N_i \right) }{\partial x'}
\end{array}\right]
{\bf q }{\bf R}_i$](img142.gif) | (35) |
where the derivatives of the shape functions with respect to the lamina coordinate system are given by
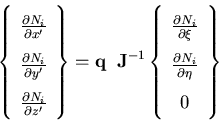 | (36) |
Next: Mass Matrix Up: Three Dimensional Element Mechanics Previous: Kinematic Description A. Zeiny
2000-09-06 
![$\displaystyle \sum_{i=1}^{n} \left[ \frac{\partial N_i }{\partial x'}
{\bf q} \...
...N_i \right) }{\partial x'}
{\bf q R_i} \mbox{\boldmath$\theta_i$\space }\right]$](img126.gif)
![$\displaystyle \sum_{i=1}^{n} \left[ \frac{\partial N_i }{\partial y'}
{\bf q} \...
...N_i \right) }{\partial y'}
{\bf q R_i} \mbox{\boldmath$\theta_i$\space }\right]$](img128.gif)
![$\displaystyle \sum_{i=1}^{n}\left[ \frac{\partial N_i }{\partial z'}
{\bf q} \o...
...N_i \right) }{\partial z'}
{\bf q R_i} \mbox{\boldmath$\theta_i$\space }\right]$](img130.gif)